How to create binary search tree in c#
Binary search trees are a fundamental data structure in computer science, providing efficient storage and retrieval of data. In this blog post, we’ll explore the concept of binary search trees, their properties, and implementation in C#. We’ll also provide a complete code example and an animated visualization of insertion.
Table of Contents:
- Introduction to Binary Search Trees
- Binary Search Tree Properties
- Implementing a Binary Search Tree in C#
- Insertion Operation
- Visualization of Insertion
- Conclusion
Introduction to Binary Search Trees:
Binary search trees are binary trees that store data in a hierarchical manner. Each node in the tree contains a value and has two children: a left child and a right child. The left child holds values less than the node’s value, while the right child holds values greater than or equal to the node’s value. This property enables efficient searching, insertion, and deletion operations.
Binary Search Tree Properties:
Binary search trees have the following important properties:
- If a node has a left child, the left child is the root of a binary search tree with a maximum value equal to or less than the node’s value.
- If a node has a right child, the right child is the root of a binary search tree with a minimum value equal to or greater than the node’s value.
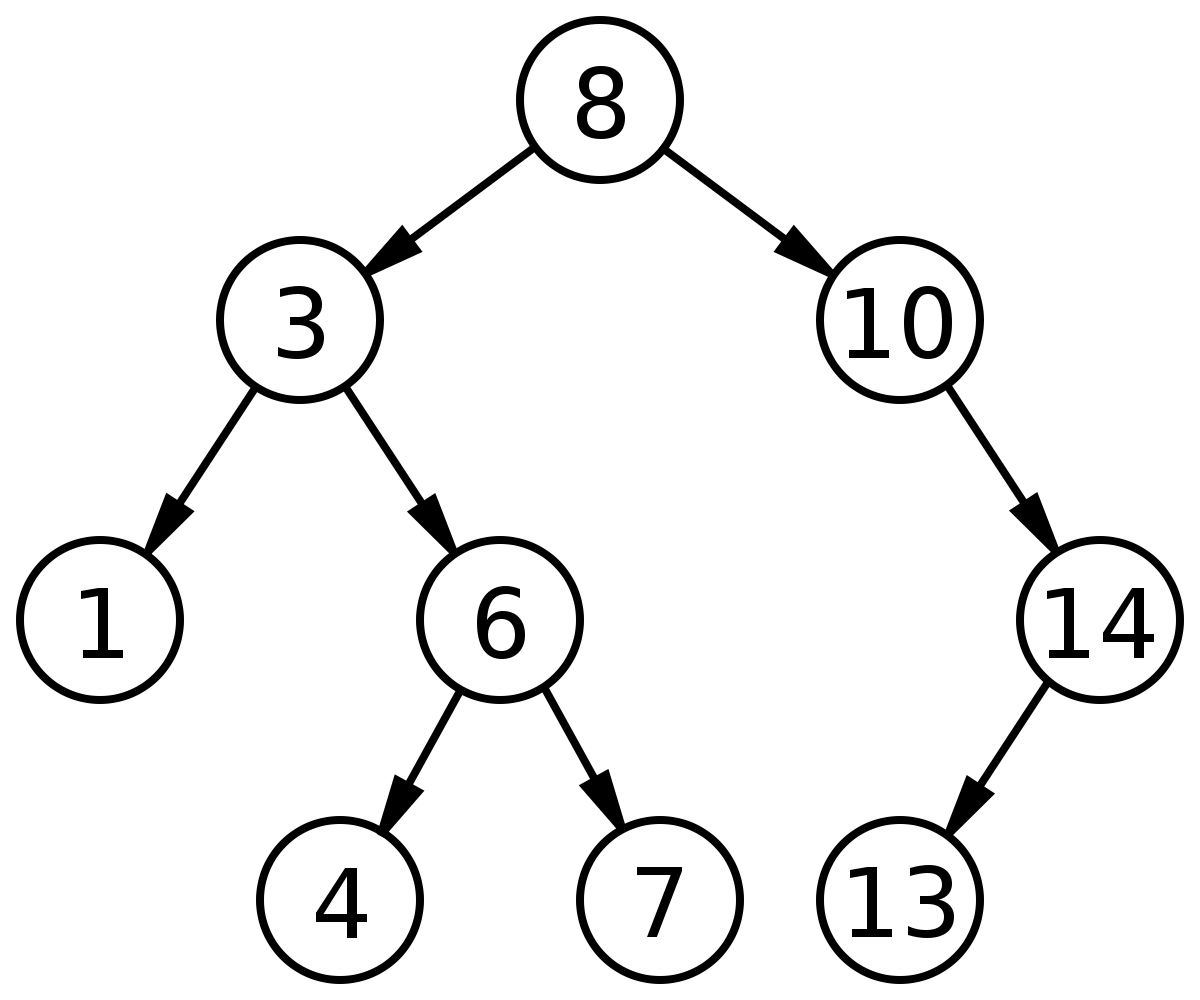
Implementing a Binary Search Tree in C#:
We can implement a binary search tree in C# using classes and recursive methods. The Node class represents a node in the tree, while the BinaryTree class handles tree operations.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace BTree
{
public class Node
{
public int Data { get; set; }
public Node Left { get; set; }
public Node Right { get; set; }
public Node()
{
}
public Node(int data)
{
this.Data = data;
}
}
public class BinaryTree
{
private Node _root;
public BinaryTree()
{
_root = null;
}
public void Insert(int data)
{
// 1. If the tree is empty, return a new, single node
if (_root == null)
{
_root = new Node(data);
return;
}
// 2. Otherwise, recur down the tree
InsertRec(_root, new Node(data));
}
private void InsertRec(Node root, Node newNode)
{
if (root == null)
root = newNode;
if (newNode.Data < root.Data)
{
if (root.Left == null)
root.Left = newNode;
else
InsertRec(root.Left, newNode);
}
else
{
if (root.Right == null)
root.Right = newNode;
else
InsertRec(root.Right, newNode);
}
}
private void DisplayTree(Node root)
{
if (root == null) return;
DisplayTree(root.Left);
System.Console.Write(root.Data + " ");
DisplayTree(root.Right);
}
public void DisplayTree()
{
DisplayTree(_root);
}
}
}
The code snippet provides the necessary classes and methods for creating and manipulating binary search trees. The Insert method inserts a new node into the tree by recursively traversing the tree until it finds the appropriate position for the new node.
The code example demonstrates how to create a binary search tree and insert values into it. After inserting values 4, 2, 5, 1, and 3, the tree structure will be built accordingly.
class Program
{
static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
Node root = new Node();
tree.Insert(4);
tree.Insert(2);
tree.Insert(5);
tree.Insert(1);
tree.Insert(3);
tree.DisplayTree();
}
}
An animated visualization can help us better understand the insertion process in a binary search tree. The animation shows how each value is inserted and how the tree structure evolves during the process. This visual representation enhances our comprehension of how the tree maintains its properties.

Conclusion
Binary search trees are a vital data structure in computer science, providing efficient storage and retrieval of data. In this blog post, we explored the concept of binary search trees, their properties, and their implementation in C#. We discussed the insertion operation and provided a complete code example along with an animated visualization of the insertion process.
Happy Coding 😊




what is the use of that node class ?
Node Class hold the node data like node value and there children